Computational Nonlinear Analysis
 Continuation is a numerical technique for computing discrete approximations of implicitly-defined manifolds, for example corresponding to parametrized families of dynamical-systems trajectories, given as the collection of solutions to a non-linear equation F(u)=0 in terms of a vector-valued function mapping F. Starting with a single chart, i.e., a point on the manifold together with a representation of the tangent space at this point, continuation employs a covering algorithm for computing nearby charts. The process is subsequently repeated for each of the nearby charts. The manifold through the initial point is called a branch or a family and the computed atlas of charts is a covering of this branch.
Continuation is a numerical technique for computing discrete approximations of implicitly-defined manifolds, for example corresponding to parametrized families of dynamical-systems trajectories, given as the collection of solutions to a non-linear equation F(u)=0 in terms of a vector-valued function mapping F. Starting with a single chart, i.e., a point on the manifold together with a representation of the tangent space at this point, continuation employs a covering algorithm for computing nearby charts. The process is subsequently repeated for each of the nearby charts. The manifold through the initial point is called a branch or a family and the computed atlas of charts is a covering of this branch.
A number of computational tools for continuation and bifurcation analysis of characteristic classes of dynamical systems trajectories have been developed in the past. Prominent examples include AUTO, MATCONT, DDE-BIFTOOL, KNUT, and LOCA.
The use of such computational tools, primarily applied to the bifurcation analysis of low-dimensional dynamical systems, has revolutionized the field of nonlinear dynamics and offers distinct advantages to brute-force forward-time simulation. Through a process of judicious exploration, such tools enable prediction of behavior and response without the need for a large collection of simulations based at distinct initial conditions. This methodology has extended the reach of methods of complex systems analysis far outside the confines of applied mathematics to a wide range of engineering, physics, chemical, and biochemistry applications.
With past support from the National Science Foundation programs for Computational Mathematics and Dynamical Systems, I was the lead investigator on a research effort called "An Algorithm Suite for Computational Nonlinear Analysis of Power Systems," whose objectives were to scale continuation methods to complex networked systems with hybrid system trajectories and tens of thousands of states, by
- developing new multiscale, multisegment, trajectory-discretization algorithms based on asynchronous collocation methods;
- developing new mesh adaptation algorithms suitable for the asynchronous collocation methods that accommodate segment-specific discretization error bounds;
- constructing domain decomposition methods particular to the network topology and the asynchronous collocation formulation that enable efficient parallel execution.
This ongoing research project builds on the Computational Continuation Core (informally known as COCO) recently documented in the extensive graduate-level textbook Recipes for Continuation, published in May 2013 by the Society for Industrial and Applied Mathematics, and through a series of video tutorials.
Upgrades to COCO included with the November 2017 release (link downloads release) enabled design optimization along families of implicitly-defined solutions to boundary-value problems. These were awarded with the First Prize in the DSWeb Competition for Software on Dynamical Systems Theory and Applications.
The most recent release of COCO from March 2020 includes support for design optimization with inequality constraints as well as continuation of multi-dimensional manifolds for problems with adaptive discretization.
- Read Zaid Ahsan's dissertation, "An adjoint-based formalism for optimal design of time-delay systems and uncertainty quantification in stochastic systems."
- Read Mingwu Li's dissertation, "Dynamics and optimal control of information transmission in complex systems."
- Read Mehdi Saghafi's dissertation, "On the application of numerical continuation to large-scale dynamical systems."
- Read Pratik Mallya's thesis, "On the problem of parallelizing manifold covering algorithms."
- Read Yuqing Wang's thesis, "Multidimensional continuation of families of periodic orbits."
- Read Erika Fotsch's thesis, "Bifurcation analysis near the cessation of complete chatter and Shilnikov homoclinic trajectories in a pressure relief valve model"
Research collaborators: Matthew West, Ian Hiskens, Frank Schilder, Mehdi Saghafi, Pratik Mallya, Maxim Markov, Mingwu Li, Erika Fotsch, Mike Henderson, Jan Sieber, Zaid Ahsan.
Complex Systems and Networks
 With support from the National Science Foundation program for Integrated NSF Support Promoting Interdisciplinary Research and Education, I was the lead investigator on the research project Asynchronous communication, self-organization, and differentiation in human and insect networks, whose objectives were the original development of a theory of parallel and asynchronous communication in complex human and insect networks and an unprecedented study of the implications of this framework for the robustness and resilience of such networks to external perturbations. The research explored the emergence of spatiotemporally correlated interaction patterns in uncoordinated, multi-agent networks and the formulation of a theoretical, experimental, and computational framework for characterizing the resultant parallel and asynchronous communication systems.
With support from the National Science Foundation program for Integrated NSF Support Promoting Interdisciplinary Research and Education, I was the lead investigator on the research project Asynchronous communication, self-organization, and differentiation in human and insect networks, whose objectives were the original development of a theory of parallel and asynchronous communication in complex human and insect networks and an unprecedented study of the implications of this framework for the robustness and resilience of such networks to external perturbations. The research explored the emergence of spatiotemporally correlated interaction patterns in uncoordinated, multi-agent networks and the formulation of a theoretical, experimental, and computational framework for characterizing the resultant parallel and asynchronous communication systems.
This highly interdisciplinary effort brought together experts in nonlinear dynamics, cognitive psychology, physics, computer science, and entomology in a high-risk venture with high-reward implications for theories of human language and communication, self-organization and differentiation in complex communication systems, and social behavior in insect colonies.
Specific research goals included:
- high-resolution characterization of spatiotemporal interaction networks of bees in an experimental hive with emphasis on mature populations as well as the emergence of structure in artificially created single-cohort colonies;
- multimodal characterization of spatiotemporal interaction and coordination networks in small and large groups of humans engaging in virtual or actual multiplayer games with emphasis on phase transitions that distinguish between failed and successful coordination; and
- development of computational algorithms and tools able to identify spatiotemporal differentiation of network agents and, in real time, long-range correlations that suggest opportunities for purposeful intervention.
A key model paradigm is that of a complex system as a filter of exogenous excitation preferentially responsive to frequencies and patterns signaling threats or opportunities. Since the complex systems of interest are networks, information of such excitation is transmitted through the system only from individual nodes to their immediate neighbors, possibly constrained by a sequential ordering of interactions in the network.
In ongoing work, we design oscillatory networks with localized nonlinearities and endogeonous energy sources. We explore the possibility that self-sustained oscillations may be triggered by brief pulses of external excitation, allowing the system to remain in a state of sustained alertness also after the excitation is removed.
- Read Mingwu Li's dissertation, "Dynamics and optimal control of information transmission in complex systems."
- Read Yu Mao's dissertation, "Modeling and design optimization of coupled and undermodeled dynamical systems."
- Download research posters (.pdf, 1.8Mb) from the 2014 and 2017 National Academies Keck Futures Initiative conferences "Collective Behavior: From Cells to Societies" and "Beyond Boundaries".
Research collaborators: Whitney Tabor, Gene Robinson, Nigel Goldenfeld, Martin Middeldorf, Tim Gernat, Vikyath Rao, Weibing Deng, Mehdi Saghafi, Russell Ritchie, Mingwu Li, Yu Mao, and two undergraduate research assistants.
Agricultural Robotics and Autonomy
 Robots are often deployed in settings where conditions are predictable and detailed knowledge of the robotic mechanism and its physical environment is available. In such circumstances, well-established robot control strategies typically guarantee successful operation over extended periods of time. When conditions are variable and unpredictable, successful deployment requires new control paradigms that adapt to uncertainty. Robotic systems for agricultural use face these very challenges. They commonly involve mobile platforms that operate across variable terrain and may require coordination over poor communication networks.
Robots are often deployed in settings where conditions are predictable and detailed knowledge of the robotic mechanism and its physical environment is available. In such circumstances, well-established robot control strategies typically guarantee successful operation over extended periods of time. When conditions are variable and unpredictable, successful deployment requires new control paradigms that adapt to uncertainty. Robotic systems for agricultural use face these very challenges. They commonly involve mobile platforms that operate across variable terrain and may require coordination over poor communication networks.
To address such challenges, the research project Cooperative Human-Robot Networks for Agricultural Applications, funded by the USDA National Institute of Food and Agriculture, and in collaboration with Deere & Co, has developed new fundamental and applied knowledge pertaining to the control of single or networked robotic manipulators on moving platforms in field environments. This research project has resulted in rigorous mathematical theory and validation using experimental data that show the successful application of a class of adaptive control designs to robotic systems, without using any detailed knowledge of the robot mechanism or the environment.
- Read Kim-Doang Nguyen's dissertation, "Stability and robustness of adaptive controllers for underactuated Lagrangian systems and robotic networks."
- Read Andres Rodriguez Reina's thesis, "Experimental validation of an L1 controller on a single robotic manipulator on a moving platform and a robotic cooperative network."
As a result of this effort, some key obstacles to the deployment of robotic manipulators in agricultural applications may be overcome. For example, the outcomes provide proof-of-concept evidence for the stable and predictable behavior of a manipulator end effector that could be used in drive-by crop inspection and treatment. Importantly, the analysis provides insight into how on-the-fly refilling of tractor-pulled seed tanks may be achieved using dedicated robotic vehicles, allowing for increased efficiency and profitability. Recent work has investigated optimal scheduling of such on-the-fly refilling vehicles in complex field operations with multiple, simultaneously-serviced planters. The knowledge gained in this ongoing research effort forms a foundation for future design and deployment of such field-scale robotic platforms.
Research collaborators: Naira Hovakimyan, Kim-Doang Nguyen, Daniel Block, Yang Li, Andres Rodriguez Reina, Christopher Marry, Zaid Ahsan, and three undergraduate research assistants.
Constrained Design Optimization
To explore and improve upon the design of an engineering system requires a combination of physical experiments and computational modeling. Physical experiments are expensive to conduct and thus limited in their ability to capture wide ranges of design choices. Computational models are cheap to analyze, but limited by an inevitable loss of realism. Reduction to a manageable computational model invariably necessitates simplifying assumptions. Of course, such simplifications may also be necessary in a physical experiment in order to keep costs down and allow a robust characterization of key performance metrics.
In the realm of computational models, sophisticated tools of analysis allow one to solve constrained optimization problems in which the design variables are chosen to optimize a key measure of system performance along a family of desired system behaviors. For example, component materials and physical dimensions may be selected in order to optimize the predicted nonlinear sensitivity of a microbeam biosensor or disturbance rejection of a floating wind turbine control architecture along families of periodic responses.
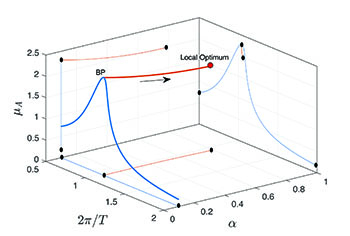 As explored by my group, control techniques may be used to support constrained design optimization also in physical experiments, including so-called software-in-the-loop tests in which parts of the physical system are modeled using computer simulations. Recent results show how adaptive control techniques allow for tracking of stable and unstable periodic responses of physical systems even in the absence of a detailed mathematical model. Parallel work has shown how uncertainty quantification using polynomial chaos can be embedded in the constrained design paradigm. Ongoing work is seeking to extend such uncertainty quantification analysis to problems with time delay, bringing together disparate branches of mathematical and computational analysis using sophisticated software tools like COCO.
As explored by my group, control techniques may be used to support constrained design optimization also in physical experiments, including so-called software-in-the-loop tests in which parts of the physical system are modeled using computer simulations. Recent results show how adaptive control techniques allow for tracking of stable and unstable periodic responses of physical systems even in the absence of a detailed mathematical model. Parallel work has shown how uncertainty quantification using polynomial chaos can be embedded in the constrained design paradigm. Ongoing work is seeking to extend such uncertainty quantification analysis to problems with time delay, bringing together disparate branches of mathematical and computational analysis using sophisticated software tools like COCO.
- Read Yu Mao's dissertation, "Modeling and design optimization of coupled and undermodeled dynamical systems."
- Read Zaid Ahsan's dissertation, "An adjoint-based formalism for optimal design of time-delay systems and uncertainty quantification in stochastic systems."
- Read Yang Li's dissertation, "Adaptive control for enhanced performance of devices and algorithms."
- Read Mingwu Li's dissertation, "Dynamics and optimal control of information transmission in complex systems."
- Read Tonghui Cui's thesis, "Optimal design of unmodeled linear systems using control-based continuation."
- Read Cole Anderson's thesis, "Robust design optimization with dynamic constraints using numerical continuation."
Research collaborators: Yang Li, Tonghui Cui, Zaid Ahsan, Mingwu Li, Cole Anderson, Yu Mao, Jan Sieber.